Banach Tarski, le début

9 août 2013

"Un anagramme intéressant de Banach Tarski est Banach Tarski Banach Tarski".

Le paradoxe de Banach Tarski, qu'est ce que c'est ?

Notre encylopédie préférée (si, si) nous répond la chose suivante : " Il est possible de couper une boule de l'espace usuel ${\R^3}$ en un nombre fini de morceaux et de réassembler ces morceaux pour former deux boules identiques à la première, à un déplacement près."

En gros, on a cette situation :

Voilà l'idée. Comment est ce possible, puisque tout physicien digne de ce nom vous dira que c'est impossible d'effectuer cette manipulation sur, disons une pomme ? (Mais vous n'aurez guère plus de chance avec un citron).

En fait, ce n'est pas toujours possible d'effectuer de tel décomposition. Par exemple, c'est impossible dans le plan. En revanche, dans l'espace, si on prends deux sous-ensembles bornés, à l'aide uniquement de rotations, il est possible de découper le premier ensemble (avec un nombre fini de morceaux !), de les déplacer à l'aide de ces même rotations et de retomber sur le deuxième ensemble ! Même si le premier est plus gros que le deuxième, parfaitement !

On va donc caractériser de tel ensemble. Les "déplacements" seront des éléments d'un groupe (par exemple, le groupe SO(3) des rotations de centre O dans l'espace).

X est dit G-dédoublable s'il existe deux parties disjointes de X, disons A et B, tel que A ~ X et B ~ X sous l'action de G. (Ici, ~ veut dire qu'on peut découper A en un nombre fini de morceaux, et déplacer chacun de ces morceaux pour qu'ils arrivent sur B grâce à des éléments de G). On voit que si un tel ensemble X existe, ainsi que le groupe G, on peut découper X, déplacer les morceaux et obtenir deux copies de X !

On va voir que certains ensembles sont dédoublables. Il y a tout d'abord l'ensemble vide qui est dédoublable sous l'action de n'importe quel groupe, ou encore le segment ]0,1[ qui est dédoublable sous l'action des homotéthies. Mais ceci n'a rien de très impressionant, puisque les homothéties de rapport non nul ne conservent pas en général le volume.

On peut dédoubler des ensembles de polynômes dans le plan complexe, sous l'action du groupe des isométries de R² (si, si, je vous jure ...) et c'est le Paradoxe de Sierpinski-Mazurkiewicz. Ce n'est plus totalement évident, et on commence à s'approcher du paradoxe en lui même. Mais le coeur même du paradoxe de Banach Tarski réside dans cette proposition :

Soit G un groupe libre de rang 2. Alors G est G-dédoublable.

Soit H un tel groupe. Dire que H est de rang 2 signifie qu'il existe a, b tel que tout éléments de H puisse s'écrire comme "mot" composé de lettre, autrement dit si tel que et qu'on ait ou , . Nos lettres sont donc a, a⁻¹, b et b⁻¹. On dit de plus qu'un mot est simplifié si il n'y a pas de lettres qui s'annulent, autrement dit de trucs du genre aa⁻¹, etc. Dire que H est libre, ça signifie que tout mot simplifié contenant au moins une lettre n'est pas égal à l'élément neutre. En particulier, H n'est pas abélien (sinon le mot simplifié aba⁻¹b⁻¹ serait égal à l'identité).

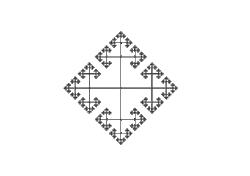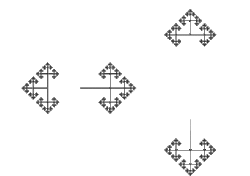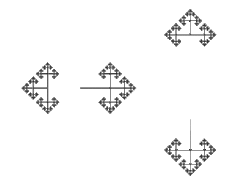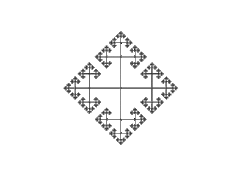
On va montrer que H est dédoublable, et dorénavant on se s'occupera plus du l'élément neutre e. H est donc l'ensemble des mots (simplifié donc) qui commencent par a, a⁻¹, b ou b⁻¹. On va donc appeller ces quatres ensembles S(a), S(b), S(a⁻¹) et S(b⁻¹). Que peut-on dire de la deuxième lettre des mots de S(a) ? Comme le mot est de la forme et qu'il est simplifié, notre deuxième lettre ne peut pas être égale à a⁻¹, sinon notre mot ne serait pas simplifié. Ensuite, on prends l'ensemble a⁻¹S(a) , autrement dit les mots de la forme . On obtient immédiatement que aS(a⁻¹) est l'ensemble de tout les mots qui ne commencent pas par a⁻¹. Donc on a a⁻¹S(a) = S(a) U S(b) U S(b⁻¹). Ainsi, S(a⁻¹) U a⁻¹S(a) engendre la totalité des mots, et donc H = S(a⁻¹) U a⁻¹S(a). Comme par le même argument S(b⁻¹) U b⁻¹S(b) = H, on obtient bien que H est dédoublable. On peut observer ici le phénomène en image :