"Bonjour, désolé de vous réveiller à une heure si matinale ... vous avez déménagé."
"Ah bon ?? Mais ... où ??"
"Dans un espace projectif..."
"Quelle drôle d'idée !"
"C'est pas moi qui décide vous savez."
"Mais alors ... J'aurais besoin d'une coordonnée supplémentaire par rapport à la terre ! Et aussi d'une carte affine pour mieux me repérer !! Heureusement que j'ai lu le fantastique de la taupe mathématicienne! Ainsi, je suis prêt pour ce voyage ! En avant l'aventure !"
J'espère que ce dialogue ô combien réaliste vous fera comprendre l'importance de bien connaître les espaces projectifs !
Premièrement : se repérer
Supposons qu'on soit sur la droite réelle projective (commencons simple !). On va utiliser un nouveau système de coordonnés baptisé coordonnées de Plücker. Pour se repérer, on sait qu'un point de 
représente une droite. Donc si je suis sur un point, je peux donner les coordonnées du vecteur sur lesquels je suis : ainsi, je suis sur )
désigne bien un point de . Pour avoir l'unicité de l'écriture, on peut regarder la deuxième coordonné : si elle n'est pas nulle, on peut considérer que les couples )
avec 
désignent bien la totalité des points de mis à part le point représentant la droite verticale et donc on rajoute le point )
traditionnellement considéré comme le point à l'infini de . On a donc décrit l'ensemble des points de comme %5Cmid%20k%20%5Cin%20%5Cmathbf%7BR%7D%20%5C%7D%20%5Ccup%20(1%5C%20%3A%20%5C%200))
où le premier ensemble s'identifie naturellement à 
et le deuxième comme le "point à l'infini".
On peut voir k comme dans le dessin ci dessus : (Où K représente la droite d'équation x = 1)
On peut faire pareil sur le plan projectif : On écrit comme les points comme )
où )
est un vecteur non nul de 
. On peut aussi l'écrire de la même manière qu'avant considérer tout les couples de la forme )
ce qui s'identifie bien au plan. Comme on a oublié encore une fois le cas où 
, c'est un plan dans l'espace et donc une droite (projective bien sûr!) dans le plan projectif, qui s'identifie naturellement aux points )
et au point )
(le point à l'infini de la droite à l'infini ...)
De manière générale, on peut procéder de manière analogue pour un système de coordonnés dans 
.
1 Il faut trouver un hyperplan 
sympathique dans 
, i.e un espace de dimension n. (sympathique signifiant quelconque, faite selon votre goût !)
2 Remarquez qu'en associant à chaque droite 
sécante à son unique point d'intersection 
vous avez une bijection entre et)
.
3 Le point précédent vous informe que vous avez une bijection entre 
et )
.
4 Vos coordonnés sont bonnes maintenant. Par exemple, dans 
, j'obtiens les points de coordonnées )
et ici c'est un espace projectif à l'infini qu'on rajoute, donc il y aura des points de la forme )
(le plan à l'infini de 
) et aussi des points de la forme )
(le droite à l'infini du plan à l'infini) et pour finir le fameux point-à-l'infini-de-la-droite-à-l'infini-du-plan-à-l'infini j'ai nommé )
. Ouf !!
Ceci dépends bien entendu de l'hyperplan à l'infini choisi. De plus, on peut voir que s'identifie naturellement à 
.
Deuxièmement : les cartes affines
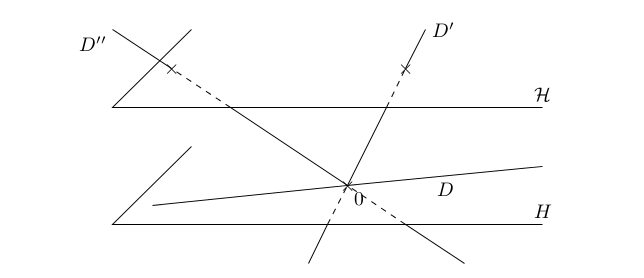
On peut détailler un peu plus la construction précédente. Soit H un hyperplan vectoriel, soit un hyperplan de direction H ne contenant pas l'origine (donc en particulier différent de H). On construit une bijection entre les droites qui ne sont pas contenus dans H et .
On appelle l'application %20%5Cbackslash%20P(H)%20%5Crightarrow%20%5Cmathcal%7BH%7D)
une carte affine. Elle permet de passer du projectif à l'affine.
On peut recouvrir un espace projectif avec des cartes affines (au minimum, n+1 cartes affines).
On peut aussi faire l'inverse : Partir d'un espace affine 
, le plonger comme hyperplan d'un espace plus gros. On choisit une origine sur qui devient ainsi un espace vectoriel 
. Ainsi, on a plongé dans 
. (Où 
est identifié à ). On peut de la même manière qu'avant identifer et %20%5Cbackslash%20P(%5Cmathbf%7BE%7D))
. )
est appellé l'hyperplan à l'infini de .
Troisièmement : repère projectifs
Bon c'est bien beau tout ça, mais si vous voulez allez à la boulangerie ... Comment faire ?? L'idéal serait quand même de se repérer.
On a un repère barycentrique si l'espace est affine, et une base si l'espace est un espace vectoriel.
On aimerait bien disposer d'un repère sur , qu'on suppose de dimension n.
On pourrait penser que si )
est une base de , un candidat pour un repère de serait )
où 
désigne la droite engendré par le vecteur 
. Le souci est que ce système de coordonnées DÉPENDS de la base choisie : en effet, on peut prendre une famille non nulle de scalaire )
dont au moins deux sont différents, alors les 
forment aussi une base mais les coordonnées homogènes associés ne seront pas les mêmes (même à multiplication près) !!
Une idée serait donc de piocher des points directements dans .
On se donne donc n+1 points )
tel que les droites )
engendrent (à l'origine près bien sûr). Là encore, même en prenant un vecteur dans chaque droite, les scalaires ne suffisent pas, à cause de l'argument précédent. Mais que se passe il si on ajoute un point )
? Ça change la vie !! (Et résoud notre problème) ! En effet, on remarque ici que l'argument précédent est invalide puisqu'une fois que notre point 
est fixé, on ne peut également plus changer aucun des 
.
En effet, soit 
un point de l'espace projectif, et )
les vecteurs associés. Si )
sont d'autre vecteurs associés à , on sait que 
. Mais d'après la définition de 
et de la liberté de la famille on obtient immédiatement l'égalité 
.
Ainsi, les coordonnés homogènes sont dans le premier cas )
et dans le deuxième cas )
ce qui définie bien les mêmes coordonnées.
Quatrièmement : étude du birapport
Revenons aux transformations projectives (qu'on appelle aussi homographie). Si %20%3D%20w)
, on peut définir %20%3D%20%5Clangle%20w%20%5Crangle)
(bien définie si f est injective).
On peut voir que l'image d'un repère projectif est un repère projectif, et que pour deux repères projectifs il existe une seule homographie qui envoie l'un sur l'autre.
On peut a présent définir une notion centrale en géométrie projective, le birapport : dans la droite projective réelle, soit a,b et c des points. Il existe une unique homographie 
tel que %20%3D%20%5Cinfty)
, %20%3D%200)
et %20%3D%201)
. On définit alors le birapport de a,b,c,d (noté 
) comme )
.
Faisons une petite disgression et revenons à la géométrie euclidienne. Est ce que donné deux points 
d'une droite et 
d'une autre, existe il une isométrie qui envoie 
sur 
? La réponse est oui si et seulement si %20%3D%20d(y_1%2Cy_2))
.
A présent étant donné 3 points 
et 3 autres points 
, existe il une similitude qui envoie sur ? La réponse est oui si et seulement si
%7D%7Bd(x_1%2Cx_3)%7D%20%3D%20%5Cfrac%7Bd(y_1%2Cy_2)%7D%7Bd(y_1%2Cy_3)%7D)
(conservation du rapport de longueur).
La propriété la plus importante du birapport est la suivante :
Soient 
des points d'une droite projective (les 3 premiers étant distincts) et 
des points d'une autre droite projective (les 3 premiers points sont encore distincts).
Pour qu'il existe une homographie 
tel que les 
soient envoyés sur les il faut et il suffit que 
= 
..
Le birapport peut aussi s'écrire : ![[\alpha, \beta, \gamma, \delta] = \frac{(\alpha - \gamma)(\beta-\delta)}{(\alpha - \delta)(\beta-\gamma)}\cdot](http://upload.wikimedia.org/math/c/5/7/c57e781917fba53795460ed016c7086a.png)
(les lettres grecques étant des nombres complexes.)
Bon sur ce, je viens d'apprendre que j'ai encore déménagé sur un espace hyperbolique, je vais essayer de voir si j'arrive à m'adapter ...
/http%3A%2F%2Fchart.apis.google.com%2Fchart%3Fchf%3Dbg%2Cs%2Cfffff0%26cht%3Dtx%26chl%3D%5Cmathbf%7BE%7D)
/https%3A%2F%2Fstorage.canalblog.com%2F59%2F11%2F1154308%2F89532560_o.png)
/https%3A%2F%2Fstorage.canalblog.com%2F47%2F67%2F1154308%2F89531442_o.png)
/http%3A%2F%2Flatex.codecogs.com%2Fgif.latex%3FF_1%2C%20F_2)