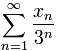Comment déménager dans un espace projectif ??
"Bonjour, désolé de vous réveiller à une heure si matinale ... vous avez déménagé."
"Ah bon ?? Mais ... où ??"
"Dans un espace projectif..."
"Quelle drôle d'idée !"
"C'est pas moi qui décide vous savez."
"Mais alors ... J'aurais besoin d'une coordonnée supplémentaire par rapport à la terre ! Et aussi d'une carte affine pour mieux me repérer !! Heureusement que j'ai lu le fantastique de la taupe mathématicienne! Ainsi, je suis prêt pour ce voyage ! En avant l'aventure !"
J'espère que ce dialogue ô combien réaliste vous fera comprendre l'importance de bien connaître les espaces projectifs !
Premièrement : se repérer
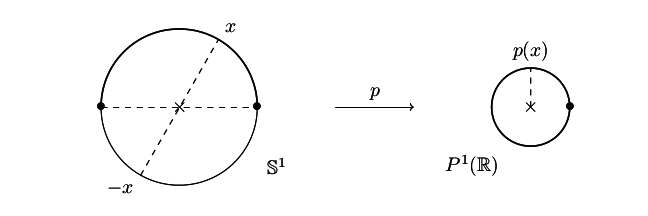
Supposons qu'on soit sur la droite réelle projective (commencons simple !). On va utiliser un nouveau système de coordonnés baptisé coordonnées de Plücker. Pour se repérer, on sait qu'un point de représente une droite. Donc si je suis sur un point, je peux donner les coordonnées du vecteur sur lesquels je suis : ainsi, je suis sur
désigne bien un point de
. Pour avoir l'unicité de l'écriture, on peut regarder la deuxième coordonné : si elle n'est pas nulle, on peut considérer que les couples
avec
désignent bien la totalité des points de
mis à part le point représentant la droite verticale et donc on rajoute le point
traditionnellement considéré comme le point à l'infini de
. On a donc décrit l'ensemble des points de
comme
où le premier ensemble s'identifie naturellement à
et le deuxième comme le "point à l'infini".
On peut voir k comme dans le dessin ci dessus : (Où K représente la droite d'équation x = 1)

On peut faire pareil sur le plan projectif : On écrit comme les points comme où
est un vecteur non nul de
. On peut aussi l'écrire de la même manière qu'avant considérer tout les couples de la forme
ce qui s'identifie bien au plan. Comme on a oublié encore une fois le cas où
, c'est un plan dans l'espace et donc une droite (projective bien sûr!) dans le plan projectif, qui s'identifie naturellement aux points
et au point
(le point à l'infini de la droite à l'infini ...)
De manière générale, on peut procéder de manière analogue pour un système de coordonnés dans .
1 Il faut trouver un hyperplan sympathique dans
, i.e un espace de dimension n. (sympathique signifiant quelconque, faite selon votre goût !)
2 Remarquez qu'en associant à chaque droite sécante à
son unique point d'intersection
vous avez une bijection entre
et
.
3 Le point précédent vous informe que vous avez une bijection entre et
.
4 Vos coordonnés sont bonnes maintenant. Par exemple, dans , j'obtiens les points de coordonnées
et ici c'est un espace projectif à l'infini qu'on rajoute, donc il y aura des points de la forme
(le plan à l'infini de
) et aussi des points de la forme
(le droite à l'infini du plan à l'infini) et pour finir le fameux point-à-l'infini-de-la-droite-à-l'infini-du-plan-à-l'infini j'ai nommé
. Ouf !!
Ceci dépends bien entendu de l'hyperplan à l'infini choisi. De plus, on peut voir que s'identifie naturellement à
.
Deuxièmement : les cartes affines
On peut détailler un peu plus la construction précédente. Soit H un hyperplan vectoriel, soit un hyperplan de direction H ne contenant pas l'origine (donc en particulier différent de H). On construit une bijection entre les droites qui ne sont pas contenus dans H et
.
On appelle l'application une carte affine. Elle permet de passer du projectif à l'affine.
On peut recouvrir un espace projectif avec des cartes affines (au minimum, n+1 cartes affines).
On peut aussi faire l'inverse : Partir d'un espace affine , le plonger comme hyperplan d'un espace plus gros. On choisit une origine sur
qui devient ainsi un espace vectoriel
. Ainsi, on a plongé
dans
. (Où
est identifié à
). On peut de la même manière qu'avant identifer
et
.
est appellé l'hyperplan à l'infini de
.
Troisièmement : repère projectifs
Bon c'est bien beau tout ça, mais si vous voulez allez à la boulangerie ... Comment faire ?? L'idéal serait quand même de se repérer.
On a un repère barycentrique si l'espace est affine, et une base si l'espace est un espace vectoriel.
On aimerait bien disposer d'un repère sur , qu'on suppose de dimension n.
On pourrait penser que si est une base de
, un candidat pour un repère de
serait
où
désigne la droite engendré par le vecteur
. Le souci est que ce système de coordonnées DÉPENDS de la base choisie : en effet, on peut prendre une famille non nulle de scalaire
dont au moins deux sont différents, alors les
forment aussi une base mais les coordonnées homogènes associés ne seront pas les mêmes (même à multiplication près) !!
Une idée serait donc de piocher des points directements dans .
On se donne donc n+1 points tel que les droites
engendrent
(à l'origine près bien sûr). Là encore, même en prenant un vecteur dans chaque droite, les scalaires
ne suffisent pas, à cause de l'argument précédent. Mais que se passe il si on ajoute un point
? Ça change la vie !! (Et résoud notre problème) ! En effet, on remarque ici que l'argument précédent est invalide puisqu'une fois que notre point
est fixé, on ne peut également plus changer aucun des
.
En effet, soit un point de l'espace projectif, et
les vecteurs associés. Si
sont d'autre vecteurs associés à
, on sait que
. Mais d'après la définition de
et de la liberté de la famille
on obtient immédiatement l'égalité
.
Ainsi, les coordonnés homogènes sont dans le premier cas et dans le deuxième cas
ce qui définie bien les mêmes coordonnées.
Quatrièmement : étude du birapport
Revenons aux transformations projectives (qu'on appelle aussi homographie). Si , on peut définir
(bien définie si f est injective).
On peut voir que l'image d'un repère projectif est un repère projectif, et que pour deux repères projectifs il existe une seule homographie qui envoie l'un sur l'autre.
On peut a présent définir une notion centrale en géométrie projective, le birapport : dans la droite projective réelle, soit a,b et c des points. Il existe une unique homographie tel que
,
et
. On définit alors le birapport de a,b,c,d (noté
) comme
.
Faisons une petite disgression et revenons à la géométrie euclidienne. Est ce que donné deux points d'une droite et
d'une autre, existe il une isométrie qui envoie
sur
? La réponse est oui si et seulement si
.
A présent étant donné 3 points et 3 autres points
, existe il une similitude qui envoie
sur
? La réponse est oui si et seulement si
(conservation du rapport de longueur).
La propriété la plus importante du birapport est la suivante :
Soient des points d'une droite projective (les 3 premiers étant distincts) et
des points d'une autre droite projective (les 3 premiers points sont encore distincts).
Pour qu'il existe une homographie tel que les
soient envoyés sur les
il faut et il suffit que
=
..
Le birapport peut aussi s'écrire : ![[\alpha, \beta, \gamma, \delta] = \frac{(\alpha - \gamma)(\beta-\delta)}{(\alpha - \delta)(\beta-\gamma)}\cdot](http://upload.wikimedia.org/math/c/5/7/c57e781917fba53795460ed016c7086a.png) (les lettres grecques étant des nombres complexes.)
(les lettres grecques étant des nombres complexes.)
Bon sur ce, je viens d'apprendre que j'ai encore déménagé sur un espace hyperbolique, je vais essayer de voir si j'arrive à m'adapter ...
Topologie des Espaces Projectifs
Je profite des vacances pour un peu regarnir ce blog qui avait quelque peu besoin de nouveaux articles !!
Comme son titre l'indique ce billet va donc parler des espaces projectifs.
Introduction
Alors un espace projectif est toujours construit à partir d'un espace (vectoriel) plus gros à la base : l'idée est de considérer des droites comme des points. En fait, c'est exactement la même démarche que notre oeil : lorsqu'on regarde le monde en 3 dimensions, on ne voit qu'un "plan" projeté sur notre rétine, on perd une dimension car à chaque droite qui passe par notre oeil n'est conservé qu'un point.
Formellement, il s'agit de prendre étant un
-espace vectoriel, de dimension n, et à considérer le quotient de
par
(vu comme groupe multiplicatif), qu'on note
. Cette définition peut sembler un peu ésotérique, mais si on regarde mieux la classe d'équivalence dans ce nouvel espace, on peut voir que
si et seulement si
,
, non nul : on voit donc qu'un point dans notre nouvel espace
correspond bien à une droite passant par l'origine dans
.
Dans la définition il est précisé également que l'espace projectif est de dimension n-1 si l'espace
de départ est de dimension n, ce qui justifie la notation de
pour un espace projectif de dimension N.
Espaces Projectifs de petite dimensions
La droite réel est associé à un seul point :
n'est donc pas très intéressant, comme on aurait pu le prévoir.
L'action pointe le bout de son nez dès qu'on prends et donc
, qu'on peut voir comme une droite étant (par définition) de dimension 1.Tout les points se trouvant sur une droite
qui passe par l'origine sont tous recollés en un seul point dans
.
On peut voir cet quotient sur le dessin suivant :
Ici l'application quotient envoie sur le point
.
Ici on voit que l'ensemble des droites du plan sont en bijection avec la moitié supérieur du cercle
, qui en fait lui même est en bijection avec le cercle
! Pour le voir, on peut aussi utiliser la "projection stéréographique" :

Il s'agit, à chaque droite passant par le point
d'associer l'unique point d'intersection avec le cercle. C'est bien une application continue et de réciproque continue. On peut se demander ou se trouve la droite associé à
: c'est la droite parallèle à l'axe
passant par ce même point, ce qui donne une petite intuition de l'idée du "point à l'infini", c'est à dire qu'on peut voir le cercle comme la droite réelle "repliée sur elle même" où
et
seraient recollés.
Le cercle étant compact, est donc compact. On verra que c'est toujours le cas. On peut aussi noter que le "point à l'infini" est un point à l'infini uniquement dans
! Pour se convaincre de cela, on peut s'imaginer qu'on aurait pu reprendre la construction du haut avec le pôle sud à la place du pôle nord du cercle. Par conséquent, l'espace projectif est un espace "homogène" : il n'y a pas de centre, et il suffit d'enlever un point à
pour qu'il redevienne homéomorphe à
, n'importe lequel !
(On peut aussi voir comme le groupe des rotations du plan autour de l'origine, puisque lui même encore en bijection avec le cercle. Il faut faire attention pour définir la bijection en question puisque la rotation de
et celle de
désigne la même droite. Cependant, on peut s'en sortir avec la racine carré et les nombres complexes, puisque pour chaque point
on peut associer deux racines distincts réglant ainsi ce problème de rotation. )
Le cas de la droite complexe est aussi très intuitif : l'espace
associé est appellé la "sphère de Riemann" et elle est homéomorphe à une ... sphère, tout simplement. On peut voir l'homéomorphisme associé avec la projection stéréographique ci dessus, où on recolle tout les bords à l'infini du plan en haut. Si on enlève un point à une sphère, on peut la déplier et retomber sur un plan.
Attention à ne pas confondre et
: ces objets ne sont pas du tout les mêmes (en effet, même si la droite complexe peut se voir comme un plan réel, au moment de quotienter le corps est différent : par conséquent le plan projectif réel est beaucoup plus compliqué à s'imaginer. Il est non-orientable, et son groupe fondamental est isomorphe à
, c'est à dire qu'il y a deux types de lacets différents sur le plan projectif!!)
Propriétés topologiques des espaces projectifs :
On peut démontrer que les espaces projectifs réels ou complexes sont toujours connexe par arcs et compacts.
Considérons le cas de : on peut voir chacune des droites
comme les deux points
et
de norme 1 par lesquels passe
. On a donc réduit le problème à trouver une quotient adapté de
. Maintenant, il suffit juste de recoller les points antipodaux, autrement dit de recoller
et
.
On obtient donc que , avec
la relation qui recolle
à
.
Cette application est fort pratique, puisqu'on obtient immédiatement que l'image d'un compact est compact, ce qui montre que tout les espaces projectifs sont compacts (pas un hasard si la droite projective s'appelle "le compactifié d'Alexandrov"...).
Pour l'argument de la connexité, on pourrait utiliser le même argument, mais il en existe un autre plus sympa : en effet, la sphère étant connexe par arcs, on peut relier les points directement dans la même hémisphère. Sinon, si
et
ne sont pas dans la même hémisphère, on peut envoyer
sur
et le problème est réglé puisque que par hypothèse il existe un chemin entre
et
.
La boîte à outils projective
Les espaces projectifs ont une structure particulière, donc en particulier ils ont leur propres morphismes. On peut le définir à l'aide des espaces vectoriels initiaux. Une application entre
et
peut être définie comme celle qui fait commuter le diagramme suivant :

Ainsi une application projective peut être uniquement définie à partir d'une application affine, qui est nécessairement injective. (Après tout, les morphismes de corps ou d'espaces métriques sont aussi nécessairements injectifs ...)
On peut encore aborder beaucoup de sujet, en particulier la relation très intéressante entre espace affine et espace projectif. Il existe notamment des repères projectifs, des coordonnées projectives (coordonnées de Plucker) des invariants projectifs (le birapport), des théorèmes beaucoup plus concis et précis énoncé comme théorème de géométrie projective ... Cependant ce sujet est plus de la géométrie que de la topologie, et il est de plus excellement expliqué dans le petit livre "Un bref apercu de la géométrie projective" par Benoît Kloenecker.
Mais bon, il se fait un peu tard, et j'aborderais sans doute ce sujet une autre fois ...
Topologies rigolotes et suite
Une suite réel, on sait tous ce que c'est : c'est une liste infinie de nombre réel, comme par exemple .
On sait tous aussi ce qu'est la limite d'une suite (si elle en admet une) quand n tends vers : c'est l'unique nombre
tel tout voisinage
contiennent tout les points de la suite
au bout d'un certain rang. Par exemple, la limite de la suite
quand n tends vers
est 0.
La notion de voisinage est définie par une distance ici, mais on peut très bien mettre une topologie (une famille d'ouvert) sur et considérer que la suite
converge vers
si tout ouvert
contenant
contient aussi tout les termes de la suite à partir d'un certain rang.
Espace non séparé :
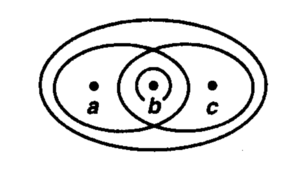
On va considérer l'ensemble suivant : muni de la topologie suivante :
. (Voir schéma dessous)
On peut alors remarquer que la suite converge vers b, mais également vers a et vers c !! En effet, le seul ouvert
qui contient a est l'ouvert
qui contient bien tout les termes de la suite à partir d'un certain rang :-)
Ici, la topologie n'a pas assez d'ouvert pour distinguer tout les points. (Les espaces de Hausdorff, ou espaces séparés, sont fait pour éviter ce genre de blague.)
Espace produits
On va considérer une famille (qui peut être infinie) d'espaces et on va noter leur produit par
. Dans le cas fini, la topologie produit peut s'écrire comme produit d'ouvert
. Dans le cas infini, on peut procéder de deux manières :
1 On écrit les ouverts de la forme : où
est ouvert dans
. Une telle topologie est appellé "box topology", qu'on notera
.
2 On écrit les ouverts de la même manière, sauf qu'ici on a sauf pour un nombre fini de valeur, et dans ce cas
est ouvert dans
.
La deuxième topologie semble un peu moins naturelle, mais on a des résultats plus cohérents avec elle. Les présentations sont faites, on va a présent passer aux résultats rigolos :
Soit . Un point
s'écrit par exemple
. On peut aussi le voir comme une suite (de
).
Maintenant, on va considérer la suite suivante (de ) , qui converge dans la topologie produit vers (0,0,0, ...) mais pas dans
!!!! :
En effet, si on prends un ouvert de de la forme :
O contient 0 et est ouvert dans . Pourtant, il n'existe aucun rang
tel que
.
Conclusion : avec ,
ne tends pas vers
(ce qui est tout à fait logique ...)
A présent, on va considérer , le sous ensemble de
tel que presque tout les termes de
soient nul, sauf un nombre fini.
Quel est l'adhérence de dans
?
Soit un point de
. Dans la topologie produit, la suite
définie par
,
, ...,
converge bien vers
(ce qui semble normal). Dans
, ça serait trop beau !!
En effet, prenons un point de
. Ce point a donc une infinité de coordonné
non nulles, sinon ce serait un point de
. Donc a présent, on peut prendre un ouvert de la forme suivante :
Où si la i-ième coordonnée est nulle, et sinon,
est un ouvert contenant
mais pas zéro (qui existe vu que
est différente de 0).
A présent, on vérifie que ne contient aucun point de
, sinon tout les points
de cet ouvert auraient une infinité de coordonnée
non nuls, ce qui est en contradiction avec la définition de
. Donc l'adhérence de
dans
avec
est
lui même.
Distance p-adique
Nous sommes a présent dans le corps des fractions. Pour chaque nombre premier p, on va définir une "valuation" (une espèce de valeur absolue, sauf qu'elle peut être négative) qui associe à un entier naturel sa puissance de p dans sa décomposition en facteur premier. On associe à
la valeur
. Par exemple,
etc...
Enfin on généralise aux fractions :

Ainsi .
Pour finir, on définit la distance ainsi obtenue :

On appelle l'espace muni d'une tel métrique.
Considérons a présent la suite dans :
Avec la topologie usuelle, elle tends évidemment vers 0. Maitenant, dans , on a
, donc
tend encore vers 0.
A présent, plaçons nous dans . On a
, et donc on obtient la jolie formule
sur laquelle je conclue ce sujet.
Le Paradoxe de Buridan (et une application du théorème du point fixe de Brouwer)
Qui est donc Buridan ? C'est un philosophe auteur du paradoxe du jour, avec ce charmant acteur ayant le rôle principal :
 petite caricature rigolote de l'époque faisant référence à Burdian
petite caricature rigolote de l'époque faisant référence à Burdian
L'âne de Buridan était un âne, qui, selon la "légende", était mort de faim et de soif, car il n'avait pas su choisir par quoi commencer entre une botte d'avoine et son seau d'eau, étant à même distance de la botte et du seau. Ce n'est pas un paradoxe à proprement parler, mais plutôt une situation intriguante puisque pourtant l'âne avait tout ce qu'il fallait à sa disposition. Cependant, ce n'est pas un paradoxe "fictif" puisqu'on peut l'observer dans la vraie vie.
Mais pourquoi cet âne n'a pas pris la nourriture la plus proche ?
Si on analyse un peu du point de vue "physique" ce qu'il se passe, on peut considérer que l'âne se trouve sur le segment , 0 et 1 représentant l'eau et l'avoine. La position de l'âne à un temps
est une fonction
qui dépend de deux chose : sa position de départ
et du temps
. Ici, on va plutôt fixer un temps et s'intéresser à ce qui se passe quand on fait varier sa position de départ. Évidemment, si l'âne commence 0 ou sur 1 son choix sera imméditament fait : on suppose donc que
et
. Selon les lois de la physique, la fonction sera continue. C'est ici que tout se joue : Si on décide que "si je commence à gauche de
, je vais à gauche, et sinon je vais à droite", cette décision n'est pas continue au point
. Des petites variations impliquent de petits changements.
étant continue, le théorème de la valeur intermédiaire nous informe qu'il y aura toujours des valeurs de
strictement entre 0 et 1.
Qu'est ce que ça veut dire : supposons qu'on attende t = 1000 ans, . On a
= 0, puisqu'au bout de mille ans, si la position intiale de l'âne était 0 il aura choisi l'eau, et si il commençait sur 1 il resterait à manger de l'avoine, et devenir gros et moche. Donc, il existe une position initiale
tel que
, avec 0 < a < 1. En particulier, au bout de 1000 ans l'âne n'aura toujours pas atteint son but, puisque si il l'avait atteint avant il serait resté dessus ! Donc, pour une durée de temps arbitraire, il existe des positions initiales tel que l'âne n'ait toujours pas pu faire de choix à la fin de ce temps. (Et en particulier, si on prends un temps suffisament élevé, notre pauvre âne a peu de chance de survivre ...)
Ainsi, de manière plus formelle et scientifique, le principe de Buridan s'énonce de la manière suivante :
Une décision discrète basé sur des informations continues ne peut pas être prise en un temps borné.
Buridan, version piétonne
On peut faire varier ce problème d'une manière intéressante. Il vous est tous arrivé dans un trottoire de vous retrouver face à une personne, et de changer de direction (aller sur la partie droite du trottoire, ou à gauche). Si deux personnes marchent l'une en face de l'autre, et doivent s'écarter au dernier moment, il existe une position initiale telle qu'elles rentrent en collision ! (en supposant qu'ils ne s'arrêtent pas)
Buridan, version céleste
Une variation de ce problème est deux pilotes d'avions qui volent : ils peuvent choisir d'aller à droite, en bas, à gauche ou à droite, et le ciel est plus large que le trottoir, donc c'est une décision continue qu'il faut prendre. La conclusion est cependant la même : si les avions ne peuvent pas s'arrêter, il existe forcément une position tel que la collision entre les deux soit inévitables.
Si on change de coordonnées, on peut se ramener au problème suivant : un avion voit un ballon volant en face de lui. On va supposer que
1) L'avion se trouve dans un plan P au début, qu'il est forcé de croiser le plan Q dans lequel est situé le ballon.
2) Si il commence très à gauche du ballon, il le contournera par la gauche. Si il commence très à droite, il ira par la droite.
On peut observer le schéma suivant :
On peut se convaincre facilement grâce à la condition 2 que si l'avion se trouve vers la ligne da, il ira par le sud, etc. Donc, l' "image" du rectangle par l'application F est envoyé sur un espace de dimension 2 homéomorphe à un rectangle et grâce au théorème du point fixe de Brouwer (chouette de la topo !!) on peut montrer qu'il existe forcément un antécédent à l'image "balloon", autrement dit une position initiale de l'avion tel qu'il percute le ballon (donc l'autre avion si on revient aux coordonnées initiales).
Buridan, version geek
On peut même avoir un apercu de ce paradoxe dans la vie de tout les jours !! En effet, supposons que lorsqu'on touche notre clavier, on envoit disons 5 volts à l'ordinateur. Si il reçoit 0 volts, on a pas appuyé sur la touche à coup sûr. Si il reçoit 5 volt, on a appuyé sur la touche à coup sûr. Maintenant, comme le fait d "appuyer sur une touche du clavier" est continue, et n'envoie pas toujours un courant constant, on peut se dire qu'il existe un intervalle (probablement très faible) ou l'ordinateur ne sait pas quoi faire (par exemple si il reçoit pile 2,5 volts ...), on ne peut pas prédire.
Conclusion
Tout en sachant que la décision discrète de fermer cette fenêtre dépends d'informations continue, il est probable qu'au moins un visiteur reste ici sur cette page à vie.
Qu'est ce que la Topologie ?
Un illustre mathématicien disait que parmi les branches des mathématiques, il y a celle qui étudiait le nombre, l'aspect arithmétique, celle qui étudiait la grandeur, l'aspect métrique (ou analytique), et celle qui étudiait la forme, l'aspect géométrique des choses. La topologie se range plutôt dans la troisième catégorie.
Au début, la géométrie s'intéressait aux figures géométriques qui possédaient certaines propriétés en communs. La géométrie s'est élargie, on a étudié des figures qui semblaient de moins en moins différentes, mais qui possédaient quand même certaines propriétés en commun. La géométrie est vue comme l'étude des transformations des figures.
La Géométrie Euclidienne
C'est la plus ancienne des géométries. On s'intéresse aux transformations qui conservent la distance, autrement dit on considère que deux figures sont équivalentes du point de vue de la géométrie euclidienne s'il existe une isométrie de
vers
. Par exemple, deux triangles congruents (qu'on peut superposer l'un sur l'autre) sont de telles figures :

La Géométrie Affine
Ensuite, on a considéré à une classe plus large de transformations : les similitudes (ou transformations affines). Ici, on exige que les rapports de longeurs soient préservés i.e, F est similaire à F' si A, B et C sont les points d'une figure F, que A', B' et C' soient les points correspondants sur la figure F', le rapport suivant soit conservé :
Autrement dit, qu'il existe une constante tel que
.
est appellé le "rapport de similitude". Par exemple, les deux figures suivantes sont alors dites semblables :

On remarque que deux figures congruentes sont toujours semblable, l'inverse n'est pas forcément vrai. La géométrie affine "englobe" donc la géométrie euclidienne. Il existe une géométrie encore plus générale :
La Géométrie Projective
Si le soleil "projette" notre ombre sur le sol plat, on a pas conservation des rapports de longeurs, notre ombre n'est pas un "réduction" de notre corps, mais certains rapports sont conservés, les birapports de longueurs. (les rapports de rapports de longueur) Sans rentrer dans les détails, ici on s'intéresse aux transformations appellées transformations de Möbius : c'est une transformation complexe de la forme : (avec ad - bc non nul)
Les déformations tolérées sont encore plus grandes, notamment n'importe quelle conique est "projectivement équivalente" à une autre ! Il en va de même pour ces deux objets en rouge :
Peut-on encore plus déformer les objets, et toujours conserver certaines propriétés ? La réponse est oui, et elle nous est donnée par la topologie.
La Topologie
 C'est ça la topologie !
C'est ça la topologie !
Pour le topologue, une tasse de café et un donut représentent le même objet. En fait, la topologie est l'étude des formes et des déformations. On l'appelle parfois "la géométrie du caoutchouc". Donc, on ne s'intéresse pas par exemple à la notion d'angle, qui est une notion géométrique. Nos figures seront des espaces. On va considérer deux espaces X et Y. On va dire que si est une bijection continue, alors on peut "déformer X continuement en Y". Si de plus,
est aussi continue, alors on peut "déformer continuement Y en X", et les deux objets sont les mêmes d'un point de vue topologique. On appelle une telle fonction un homéomorphisme. On peut remarquer que les homéomorphismes sont à la topologie ce que les similitudes sont à la géométrie affine.
Si est une bijection continue, on ne sait pas si
est un homéomorphisme. Par exemple, l'application qui envoie le segment
sur
, le cercle unitée,
est continue mais n'est pas bicontinue. Cette fonction n'est donc pas un homéomorphisme. (En fait, le cercle et le segment ne sont pas homéomorphe. L'argument le plus simple est un argument de connexité.)
Qu'est ce qu'une fonction continue ?
En fait, la notion "être continue" est très vague. Intuitivement, une fonction est continue si il n'y a pas de "déchirure", donc si f(x) peut être voisin de f(y) à condition que x et y soit voisin, pour tout x de X et pour tout y voisin de x. Cette notion étant un peu vague, il faut qu'on décide quelles fonctions sont continues, et quelles fonctions ne le sont pas. Pour ça, on va prendre notre espace , et lui ajouter une topologie
. Cette topologie est un ensemble de parties de
, qu'on appelle ouverts. Ils vérifient trois axiomes :
- si
, alors
(autrement dit, toute union d'ouverts est ouverte)
- si
alors
. (autrement dit, toute intersection finie de fermés est fermée)
A présent, qu'on a nos ouverts, on va dire que notre fonction est continue si et seulement si
, on a
i.e la préimage de tout ouvert de Y est un ouvert dans X. Nos ouverts vont jouer à peu de choses près le rôle des voisinages.
On peut voir un premier exemple avec les ouverts dans . On va définir les ouverts comme étant les ensembles :
tel que
. Comme on voit que les axiomes sont bien vérifiés, on retrouve une topologie. En particulier, la notion de fonction continue coïncide, puisque la définition de la continuité de
en
qu'on voit est :
, ce qui est exactement la définition d'un ouvert !
Les invariants topologiques
La notion de fonction continue est très importante en topologie, puisqu'on va s'intéresser au propriétés invariantes par homéomorphisme, donc que les bijections bicontinues conservent.
Notamment, la propriété d'être compact, connexe ou d'être séparé est un invariant topologique. "Être un invariant topologique" signifie que si possède cette propriété, et que
est homéomorphe à
(relation qu'on note d'habitude
), alors
la possède aussi. Conséquemment, si
possède une propriété invariante par homéomorphisme que
ne possède pas, cela signifie qu'ils ne sont pas homéomorphes.
Toutefois, il peut arriver des surprises avec des topologies, par exemple le cas d'une suite de convergente qui admet plusieurs limites (cela arrive quand il n'y a pas suffisament d'ouvert pour distinguer tout les points de l'espace
).
Le sinus du topologue
Un exemple de courbe qu'on étudie en topologie est le sinus du topologue, l'ensemble défini par : où
On obtient alors l'image suivante :

Le segment vertical à gauche représente et la courbe représente
. Sa propriété particulière est d'être connexe, d'être "d'un seul morceau" mais pas localement connexe : autrement dit, il est globalement "d'un seul morceau", mais si on zoome, même aussi près qu'on veut, près d'un point de
, on ne peut pas trouver de point
de
et un
tel que
(où
désigne le disque de rayon
>0) soit connexe : autrement dit, même en zoomant toujours, il y aura des petits bouts de droites qui ne sont pas reliés, connecté entre elles. (Faites un dessin, et dessinez cette boule : Il y aura toujours un petit bout de droite qui ne sera pas relié à
...)
Voilà donc un bref aperçu de ce qu'est la topologie ! Elle est indispensable dans des domaines tel que l'analyse, la géométrie ou la topologie algébrique (si, si ...)
Petits paradoxes de l'infini/Jeux amusants
Aujourd'hui, j'ai pas envie de faire des maths. On va jouer ! À quel jeu allons nous jouer aujourd'hui ?
Jeu n°1 :
Alors, je vous propose un marché on ne peut plus honnête. Je vous demande la somme que vous voulez, vous me la donnez. Et le lendemain, je vous rembourse le double ! Vous acceptez ? Préparez vous à être endetté pour le restant de vos jours !!!
Jour 1 : Je vous emprunte 1 €. Pas plus.
Jour 2 : Je vous emprunte 3 €. Comme je vous en devais 2, j'en met immédiatement 1 de côté et je vous rends les 2 € restants.
Jour 3: Je vous emprunte 7 €. Comme je vous en devais 6, j'en met immédiatement 1 de côté et je vous rends les 6 € restants.
Jour 4: Je vous emprunte 15 €. Comme je vous en devais 14, j'en met immédiatement 1 de côté et vous avez compris que je vais gagner 1 € par jour, jusqu'à la fin de ma vie :-)
Ce petit souci est évidemment dû à l'infini, puisque si l'arrangement était limité dans le temps, j'aurais eu un petit souci le dernier jour du contrat ...
Jeu n°2
Vous avez gagné au lotto. Tout les jours, vous allez recevoir 10 pièces de monnaie. Toute les années, je vais vous en enlevez une.
Que va il se passer à l'infini ? Est ce que vous allez être riche, ou au contraire ultra riche ???
(petite phase de suspens)
En réalité, j'affirme qu'à l'infini il ne vous restera plus rien !! On effet, on va supposer qu'il vous reste quelque chose, disons au moins une infinité de pièces, ou alors un nombre fini. Si on numérote les pièces reçus, disons seront les pièces reçues le premier jour,
les pièces reçues le deuxième jour, et ainsi de suite. On va prendre la plus vieille pièce, disons
. Or, nous somme à l'infini, en particulier nous avons dépassé l'année
, donc je vous ai déjà retiré cette pièce ... Contradiction ! Conclusion, c'était bien joli de gagner à peu près 364 pièces par an, mais si c'est pour se retrouver sans le sou à la fin, ce n'était pas vraiment utile .... ;)
Jeu n°3
On va considérer que vous faites partie d'une équipe de pirates A,B,C,D et E(mathématiciens, les bougres sont tous supers intelligents !!). Vous avez 100 pièces d'or, et le partage se fera de la manière suivante : A propose un partage qu'il juge équitable, on vote à la majorité. Si il obtient la majorité absolue, on partage de la manière proposé. Sinon, A est tué et c'est au tour de B de faire le partage. On suppose les pirates meurtriers : si ils peuvent tuer sans changer leur part potentiels, ils n'hésiteront pas. Que doit faire A ? Doit séparer sa part en 3 pour amadouer d'autre pirates ?
En fait, A peut s'en sortir avec 96% du butin !! Pas mal non ? Alors, comment on procède ? On va commencer par la fin :
1 Si E reste seul, il prends toute les pièces pour lui (ça peut sembler évident).
2 Si E et D restent en tête-à-tête, quoi que propose D, E va le tuer et prendre les 100 pièces restantes.
3 A présent, supposons qu'il ne reste que C, D et E. Si C propose une solution quelconque à E, il la refusera puisque c'est largement plus intéressant pour lui de refuser sa proposition, et de tuer C puis D. En revanche, D a tout interêt à accepter toute proposition de C, sinon il est bon se faire tuer par E ! Donc, si C reste seul avec D et E, il peut ne rien proposer à D, et s'en tirer avec 100 pièces d'or.
4 Supposons a présent que B soit en jeu. Il lui faut la majorité absolue, soit 3 voies, donc deux de plus que la sienne. B peut espérer amadouer D et E, qui seraient désavantagés si C venait à prendre une décision ! B peut donc s'en tirer avec 98 pièces.
5 A présent, supposons que vous commenciez. Vous ne pouvez évidemment pas proposer de pièces à B ou à C, qui ont meilleur temps de refuser votre offre. En revanche, vous pouvez augmenter l'offre de B, afin que ceux ci préfèrent votre partage. Vous donnez donc 2 pièces à D et E et vous vous en tirez ainsi avec 96 pièces ! Pas mal, non ?
Symétrie, groupes diédraux et autres
Suite à ma lecture du très bon "La Symétrie, ou les maths au clair de lune" de Marcu du Sautoy, j'ai décidé de parler de ... symétrie !! Bon, en fait, ce post est surtou un prétexte pour faire un (très) rapide tour des groupes, avec quelques propriétés et un poil de géométrie aussi.
Un groupe : qu'est ce que c'est ?
Alors, un groupe, on a vu ce que c'était, c'est un ensemble muni d'une loi de composition
.
Elle doit vérifier trois propriétés :
1 (on appelle cette propriété associatiativité)
2 (e est l' "élément neutre" du groupe)
3 (on souvent,
est noté
ou
, on appelle h l'inverse de g)
Ces propriétés peuvent sembler un peu abstraites, mais on peut les voir sur un exemple concret. On rappelle que c'est l'ensemble des nombres entiers, positifs, négatifs ou nul. On va prendre le groupe
, la loi + est la loi d'addition qu'on connait tous. La loi est évidemment associative, autrement dit a+(b+c) = (a+b) + c, on est tous d'accord dessus.
Maintenant, on va essayer de trouver l'élément neutre de (qu'on va noter
, on a compris que la loi associé à
est + ...). Quel est l'élément e de
tel que a + e = e + a = a ? Bon ici, la réponse semble évidente, c'est 0. De même pour l'inverse de a, cet élément est tout simplement -a .
Un groupe peut aussi admettre des plus petits groupes à l'intérieur de lui. Un sous groupe de
, c'est un ensemble
tel que
et
soit un groupe. C'est un "groupe à l'intérieur du groupe". Il est important qu'il soit stable par l'opération
, autrement dit que
si a et b sont dans
, et que
si
. Par exemple,
n'est pas un sous-groupe de
, car
.
Le groupe diédral , les symétries du triangle
A présent, on va s'intéresser à un triangle équilatéral, et aux sommets de ce triangle qu'on va appeller A, B et C. On va considérer toute les symétries du triangle, les transformations qui envoie un sommet sur un sommet. Tout d'abord, il y a l'identité (f(x) = x). On va la noter . Ensuite, il y a une rotation d'angle 60°, et une rotation d'angle 120°. On va les noter
et
. On peut déjà remarquer que
. Ensuite, on peut considérer les symétries qui laissent juste un sommet invariant : f(A) = A, f(B) = C et f(C) = B. C'est une symétrie centrale. On va l'appeller
. On voit immédiatement que
. Ensuite, on voit que
laisse invariant C, et que
laisse invariant B. On a donc 6 éléments :
. Ces 6 éléments sont l'ensemble du groupe diédral.
On peut vérifier que c'est un groupe. L'élément neutre est l'identitée, l'inverse d'une rotation est bien une rotation, et l'inverse d'une symétrie centrale est bien la symétrie centrale, donc chaque éléments possède bien un inverse. C'est la même chose pour la propriété d'associativité. On peut observer que ce groupe n'est pas abélien, autrement dit il ne vérifie pas tout le temps . Par exemple,
laisse juste C invariant, tandis que
laisse juste B invariant (on en déduit au passage l'égalité
=
), donc ce ne sont pas les mêmes éléments. On peut aussi s'entraîner à calculer la table de multiplication de
, autrement dit calculer qu'est ce que ça donne
par exemple. On trouve quatres sous-groupes dans
:
et
,
et
.
On peut généraliser les groupes diédraux : pour tout polygône régulier à n sommets, un groupes diédral lui est associé.
Le groupe symétrique
Si on a un jeu de 3 cartes, de combien de manière différentes on peut redistribuer ce jeu ? Si vous y réfléchissez un peu, celà revient à trouver toute les bijections de dans lui même. Par exemple, une manière de distribuer le jeu est
. On note cette bijection
. L'identité est notée
. La transformation f tel que f(1) = 2, f(2) = 3 et f(3) = 1 est noté
. Ces deux groupes désignent donc quelque chose de totalement différents, et pourtant ils ont également les mêmes propriétés. Par exemple, si on énumère la liste des éléments de
:
. Qu'est ce qu'on peut remarquer ? Le
et autres
laissent un chiffre invariant et en permute deux. Tiens, tiens, ça me rappelle quelque chose là ... Quand à
ça rappelle étrangement les rotations d'un sommet d'un triangle ... Si de plus, on remarque que ce groupe est non abélien (
mais
) et que les sous-groupes de
ressemblent furieusement à ceux de
... Mais oui,
=
! (On note plutôt
d'habitude).
La notion d'isomorphisme
Quand deux groupes et
se "ressemblent furieusement", on dit qu'il sont isomorphes. Qu'est ce que ça veut dire, être isomorphes ? Ça veut dire qu'à chaque élément
, il va y avoir un élément
qui "joue le rôle de g dans
". Par exemple ici, on va avoir une correspondance entre
et
.
De manière plus formelle, on va appeller un morphisme ou homomorphisme de groupe une application tel qu'on ai tout le temps l'égalité suivante :
. Intuitivement,
représente le même élément que
. S'il est bijectif, on appelle ce morphisme un isomorphisme. Deux groupes sont donc dit isomorphes si il existe une telle application.
C'est important que le morphisme soit bijectif pour que les groupes soient considérés comme "isomorphes", par exemple l'application qui envoie un groupe sur l'élément neutre d'un autre groupe est un morphisme, mais celà ne signifie absolument pas que les groupes sont "les même" ...
On voit que certaines propriétés sont conservées grâce aux morphismes, par exemple si A est abélien et isomorphe à B, B est abélien.
Pour revenir à et
, on peut "construire" un isomorphisme en envoyant un élément de
sur un élément de
, un par un. Dans le cas général, c'est plutôt une mauvaise idée, et on préfère utiliser certains théorèmes qui servent à ça (les théorèmes d'isomorphismes).
Cantor, j'adore.
"Léo, j'ai besoin de ton aide là ... J'arrive pas à voir pourquoi, en dimension infinie, il y a pas de surjections de V dans V*... "
"Bah c'est tout simple. Il suffit d'utiliser la diagonale de Cantor. C'était vraiment super simple, tu construis une fonction [....]"
"Ah, oui ..."
Cette conversation a eu lieu il y a quelques jours, et je me suis rendu compte qu'on pouvait dériver cet argument quelques fois, tout simple mais il fallait y penser. Cet argument est quand même un indispensable de la démonstration en mathématiques, et il est utilisé pas mal de fois. L'idée est la suivante : On veut trouver un élément particulier d'un ensemble, qu'on va construire à partir d'une liste, pour obtenir certaines propriétés qui découleront de sa construction. On s'intéresse pour cela à la diagonale d'un ensemble, définie par toute les couples .
La non dénombrabilité de R
C'est la fois ou cet argument a été utilisé la première fois, par Cantor. Il fourni la preuve que n'est pas en bijection avec
. (On va se contenter de montrer qu'il n'existe pas de surjection de
dans
. Soit
une telle surjection. On va construire un élément de
de
. Si une telle surjection existe, alors il existe une suite
tel que
. En particulier, on va prendre le dévellopement décimale de chaque terme de la suite :
Par exemple, ...,
...., etc ... A présent, on va construire
de la manière suivante :
si
, et
sinon.
Une fois qu'on a construit notre nombre on constate qu'il appartient à
et qu'en plus, il ne peut pas être dans la liste, puisque si on avait
pour un certain i, on aurait notamment
ce qui est impossible. Le nom de "diagonale" vient du fait que si on écrit dans un tableau les
, ils représentent la diagonale du tableau (les indices ne sont pas les même mais on voit la diagonale qui apparait ) :

La non-dénombrabilité de l'ensembe triadique de Cantor
On prends le dévellopement en base 3 des éléments de C, on suppose qu'ils sont dénombrables et utilise exactement le même argument ! Tout simplement !
L'existence d'un nombre complexe transcendant de module 1
Supposons que pour les besoins d'un certain paradoxe d'un certain polonais (Oui ! Bien sûr, vous avez tous reconnu le paradoxe de Sierpinski-Mazurkiewicz !) on ait besoin d'un nombre complexe transcendant de module 1, autrement dit un nombre z qui ne soit solution d'aucun polynôme complexe rationnel, et de module 1.
(On va dire qu'ici, dénombrable signifie infini-dénombrable, donc en bijection avec ).
Si on définit , on voit bien que
parcours l'ensemble des polynômes complexes rationnels de degré 1. C'est la réunion de deux ensembles dénombrables, donc
dénombrable.
Si on définit de même manière , qui contient l'union possible des n couples de rationnels, on voit qu'
peut être associé à l'ensemble des polynômes de degré n, et
est dénombrable aussi. (En fait, toute union dénombrable d'ensemble
dénombrable est dénombrable. Si on désigne par
le j-ième élément de
, On sait que
est dénombrable, et il suffit pour chaque ensemble dénombrable
d'associer le couple
au couple
. Ainsi, chaque élément
possède un unique couple associé
. Donc
peut être mis en bijection avec
, donc E est dénombrable.
Grâce à cet argument, on peut voir que l'union des est dénombrables.
A présent qu'on a une liste dénombrable des polynômes complexes rationnels, on a aussi une liste dénombrable de leur raçine ! Donc, en éliminant des doublons et en ne prenant que les nombres de module 1, on a obtenu LA suite des nombres algébrique de module 1 ! Eh oui, chouette suite n'est ce pas ?
Surtout qu'a présent, vous avez compris le principe, on va diagonaliser la suite, mais on va utiliser une petit astuce avant ... (Bah oui, qui nous dit que le nombre obtenu en "cantorisant" la suite sera aussi de module 1 ? ) En fait, on va utiliser une petite astuce, et considérer la bijection : . On va prendre notre suite
des nombres algébriques de module 1, et prendre la suite correspondante
tel que
si on applique la méthode de la diagonale de Cantor à la suite
, on peut exhiber un élément
dont
. En particulier,
est un nombre complexe, de module 1 et transcendant. On a fini par le trouver !!
Le dual en dimension infinie
Pour détailler un peu le premier exemple, va prendre un K-espace vectoriel de dimension infini (chouette, un K-espace vectoriel
de dimension infini !!). On considère son dual,
. Le dual
d'un espace vectoriel
est l'ensemble des formes linéaires, autrement dit des applications
. Le dual est aussi un espace vectoriel, et les vecteurs de
sont ces mêmes applications. En dimension finie,
et
sont isomorphes (ça veut juste dire qu'ils ont la même dimension), mais seulement, quand on passe à la dimension infinie, ça ne marche plus !
devient beaucoup plus gros que
, et il n'existe pas de surjection de
dans
! Ici encore, l'argument de la diagonale de Cantor va nous sauver ! On va prendre une base arbitraire de
, disons
. On va aussi prendre une base arbitraire de
,
. On construit une fonction
de la manière suivante :
, i.e
si
est non nulle, et
sinon. Ainsi,
n'a pas de préimage, et donc il n'existe pas de surjection de
vers
.
Donc pour résumer ... La diagonale de Cantor, j'adore !!
Fantastique Ensemble de Cantor !
L'ensemble triadique de Cantor, c'est un super objet, source de contre-exemple et aussi de propriétés surprenantes.
On le définit de la manière suivante : on va prendre le segment [0,1], auquel on va enlever le tiers central. On obtient deux segments, auquel on va aussi enlever le tiers central. On recommence à chaque étape. Si on appelle l'ensemble l'ensemble obtenu à chaque étape, on définit l'ensemble de Cantor C comme
. Visuellement, ça donne ça :

On peut aussi également voir cet ensemble comme tout les nombres qui admettent un dévellopement décimal en base 3 uniquement avec des 0 et des 2 : x ressemble à quelque chose comme
On a défini l'ensemble de Cantor. On peut voir plusieurs propriétés intéressantes, notamment :
Sa mesure est nulle. En effet, on a . On peut remarquer que la mesure de l'ensemble de Cantor, c'est 1 moins la mesure des segments qu'on enlève, et donc
C est un ensemble indénombrable. En effet, on peut utiliser l'argument de la diagonale de Cantor ici : si on peut dénombrer C, on peut écrire une liste :
. On va considérer
défini de la manière suivante :
si
, et
sinon. De cette manière, on voit que clairement
, mais que si b ne peut être égal à aucun des
puisqu'il a la n-ième décimale qui diffère avec ce nombre.
On peut prouver un résultat fort sympathique en admettant les lemmes suivants : toute partie de admet une base dénombrable, toute partie fermée de l'ensemble de Cantor est un rétract de C (une partie plus petite que C sur laquelle C peut se "rétracte continuement"), tout application continue d'un rétract de X vers Y admet une extension continue de X vers Y.
On peut a présent énoncer ce théorème : Tout compact K de est l'image continue de l'ensemble de Cantor !
Pour montrer qu'il existe une tel application continue, on va en fait construire une surjection d'un rétract de C dans notre compact K, et ensuite étendre cette application.
Pour construire une surjection pareil, on va d'abord observer qu'il existe une base dénombrable de ce compact K, . Une base dénombrable, ça veut dire que si je veux trouver un ensemble de rayon
et qui contient un point x donné, je peux.
admet une base dénombrable : toute les boules ouvertes à centre rationnel et à rayon rationnel strictement positif. On voit que cet ensemble est dénombrable, et qu'il peut bien être aussi proche qu'on veut de n'importe quel point. Maintenant, on prends une famille de fonction
, où P(K) désigne l'ensemble des parties de K, qu'on défini de la manière suivante :
et
. Donc, notre fonction va associer à 0 ou à 2 des parties de la base dénombrables de K. Maintenant, on considère la fonction g, qui associe à x le point
si il existe. La fonction n'est pas définie sinon.
Pour comprendre à quoi ressemble cette fonction, on peut s'imaginer les comme des ouverts qui recouvrent entièrement notre compact, et qui peuvent également s'approcher arbitrairement de n'importe quel point.
représente soit l'adhérence de l'ouvert
, soit son complémentaire. Maintenant, si il existe n et m tel que
(que les ensembles associés soient disjoints), la fonction g n'est pas définie. Sinon, si la fonction est définie, celà signifie que tout
contient le point p(x). Si on prends un point q disjoint de p, il existe un i tel que
ou alors
. Donc si
, on voit qu'il n'y a au maximum qu'un seul point, donc que g est bien définie.
On a a présent une fonction : . Si on prends un point p de K, on a forcément p qui appartient à
ou à
. Il ne peut pas appartenir à l'un et l'autre. Si on prends le point x, qu'on définit de la manière suivante :
si
, et
sinon. On voit que l'image de x par la fonction g est le point p, donc g est surjective. Pour voir qu'elle est continue, on va prendre un point x de C et
. Il existe
tel que
et
. On va prendre y tel que g(y) soit définie et
. Alors, on a toute les premières décimales de y qui sont communes à celle de x, et donc en particulier
et donc en particulier
si
. D'où la continuité de g. Pour conclure le théorème, on va juste montrer que A, le domaine de définition de la fonction g, est bien fermé. On va étudier son complémentaire, l'ensemble des points tel que
. Soit x un tel point. On peut remarquer que
est un recouvrement ouvert de X (l'égalité a été obtenu par passage au complémentaire). Il existe donc un nombre fini d'ouvert, et en particulier un rang m tel que
. Si on repasse au complémentaire, on obtient que
. En particulier, si
alors on a aussi g(y) qui n'est pas défini. Donc le complémentaire de A est ouvert dans C, ainsi A est bien fermé dans C. Ainsi, par les lemmes successifs, A est un rétract de C, et donc g admet une extension continue de C dans K. Ainsi tout compact est bien l'image continue de l'ensemble de Cantor.
Une conséquence immédiate est le théorème suivant : , le cube
est l'image continue de l'ensemble de Cantor, et donc de
par extension (qui vient du théorème de Tietze celle là).
Donc autrement dit, on peut déformer continûment le segment [0,1] pour obtenir un hypercube de dimension quelconque !! C'est pas complètement dingue ça ?
Il existe encore une généralisation de ce théorème, plus puissante, le théorème de Hahn Mazurkiewicz : tout espace K dans est compact, locallement connexe et connexe si et seulement il existe une fonction continue :
tel que
.
(Personnellement j'étais très surpris quand j'ai découvert ce théorème, même si je connaissais déjà un peu la courbe de Peano et ses copains...)
L'ensemble de Cantor n'a pas fini de nous surprendre : il y a également l'espace de Cantor, le carré de Cantor, le cube de Cantor, l'escalier de Cantor, le tipi de Cantor, ....