Fantastique Ensemble de Cantor !
L'ensemble triadique de Cantor, c'est un super objet, source de contre-exemple et aussi de propriétés surprenantes.
On le définit de la manière suivante : on va prendre le segment [0,1], auquel on va enlever le tiers central. On obtient deux segments, auquel on va aussi enlever le tiers central. On recommence à chaque étape. Si on appelle l'ensemble l'ensemble obtenu à chaque étape, on définit l'ensemble de Cantor C comme
. Visuellement, ça donne ça :

On peut aussi également voir cet ensemble comme tout les nombres qui admettent un dévellopement décimal en base 3 uniquement avec des 0 et des 2 : x ressemble à quelque chose comme
On a défini l'ensemble de Cantor. On peut voir plusieurs propriétés intéressantes, notamment :
Sa mesure est nulle. En effet, on a . On peut remarquer que la mesure de l'ensemble de Cantor, c'est 1 moins la mesure des segments qu'on enlève, et donc
C est un ensemble indénombrable. En effet, on peut utiliser l'argument de la diagonale de Cantor ici : si on peut dénombrer C, on peut écrire une liste :
. On va considérer
défini de la manière suivante :
si
, et
sinon. De cette manière, on voit que clairement
, mais que si b ne peut être égal à aucun des
puisqu'il a la n-ième décimale qui diffère avec ce nombre.
On peut prouver un résultat fort sympathique en admettant les lemmes suivants : toute partie de admet une base dénombrable, toute partie fermée de l'ensemble de Cantor est un rétract de C (une partie plus petite que C sur laquelle C peut se "rétracte continuement"), tout application continue d'un rétract de X vers Y admet une extension continue de X vers Y.
On peut a présent énoncer ce théorème : Tout compact K de est l'image continue de l'ensemble de Cantor !
Pour montrer qu'il existe une tel application continue, on va en fait construire une surjection d'un rétract de C dans notre compact K, et ensuite étendre cette application.
Pour construire une surjection pareil, on va d'abord observer qu'il existe une base dénombrable de ce compact K, . Une base dénombrable, ça veut dire que si je veux trouver un ensemble de rayon
et qui contient un point x donné, je peux.
admet une base dénombrable : toute les boules ouvertes à centre rationnel et à rayon rationnel strictement positif. On voit que cet ensemble est dénombrable, et qu'il peut bien être aussi proche qu'on veut de n'importe quel point. Maintenant, on prends une famille de fonction
, où P(K) désigne l'ensemble des parties de K, qu'on défini de la manière suivante :
et
. Donc, notre fonction va associer à 0 ou à 2 des parties de la base dénombrables de K. Maintenant, on considère la fonction g, qui associe à x le point
si il existe. La fonction n'est pas définie sinon.
Pour comprendre à quoi ressemble cette fonction, on peut s'imaginer les comme des ouverts qui recouvrent entièrement notre compact, et qui peuvent également s'approcher arbitrairement de n'importe quel point.
représente soit l'adhérence de l'ouvert
, soit son complémentaire. Maintenant, si il existe n et m tel que
(que les ensembles associés soient disjoints), la fonction g n'est pas définie. Sinon, si la fonction est définie, celà signifie que tout
contient le point p(x). Si on prends un point q disjoint de p, il existe un i tel que
ou alors
. Donc si
, on voit qu'il n'y a au maximum qu'un seul point, donc que g est bien définie.
On a a présent une fonction : . Si on prends un point p de K, on a forcément p qui appartient à
ou à
. Il ne peut pas appartenir à l'un et l'autre. Si on prends le point x, qu'on définit de la manière suivante :
si
, et
sinon. On voit que l'image de x par la fonction g est le point p, donc g est surjective. Pour voir qu'elle est continue, on va prendre un point x de C et
. Il existe
tel que
et
. On va prendre y tel que g(y) soit définie et
. Alors, on a toute les premières décimales de y qui sont communes à celle de x, et donc en particulier
et donc en particulier
si
. D'où la continuité de g. Pour conclure le théorème, on va juste montrer que A, le domaine de définition de la fonction g, est bien fermé. On va étudier son complémentaire, l'ensemble des points tel que
. Soit x un tel point. On peut remarquer que
est un recouvrement ouvert de X (l'égalité a été obtenu par passage au complémentaire). Il existe donc un nombre fini d'ouvert, et en particulier un rang m tel que
. Si on repasse au complémentaire, on obtient que
. En particulier, si
alors on a aussi g(y) qui n'est pas défini. Donc le complémentaire de A est ouvert dans C, ainsi A est bien fermé dans C. Ainsi, par les lemmes successifs, A est un rétract de C, et donc g admet une extension continue de C dans K. Ainsi tout compact est bien l'image continue de l'ensemble de Cantor.
Une conséquence immédiate est le théorème suivant : , le cube
est l'image continue de l'ensemble de Cantor, et donc de
par extension (qui vient du théorème de Tietze celle là).
Donc autrement dit, on peut déformer continûment le segment [0,1] pour obtenir un hypercube de dimension quelconque !! C'est pas complètement dingue ça ?
Il existe encore une généralisation de ce théorème, plus puissante, le théorème de Hahn Mazurkiewicz : tout espace K dans est compact, locallement connexe et connexe si et seulement il existe une fonction continue :
tel que
.
(Personnellement j'étais très surpris quand j'ai découvert ce théorème, même si je connaissais déjà un peu la courbe de Peano et ses copains...)
L'ensemble de Cantor n'a pas fini de nous surprendre : il y a également l'espace de Cantor, le carré de Cantor, le cube de Cantor, l'escalier de Cantor, le tipi de Cantor, ....

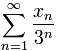


/http%3A%2F%2Fchart.apis.google.com%2Fchart%3Fchf%3Dbg%2Cs%2Cfffff0%26cht%3Dtx%26chl%3D%5Cmathbf%7BE%7D)
/http%3A%2F%2Fstorage.canalblog.com%2F59%2F11%2F1154308%2F89532560_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F47%2F67%2F1154308%2F89531442_o.png)
/http%3A%2F%2Flatex.codecogs.com%2Fgif.latex%3FF_1%2C%20F_2)